The Discrete Time Fourier Transform (DTFT) can be viewed as the
limiting form of the DFT when its length ![]() is allowed to approach
infinity:
is allowed to approach
infinity:
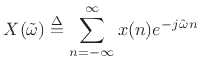
where
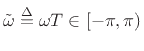 denotes the continuous
normalized radian frequency variable,B.1 and
denotes the continuous
normalized radian frequency variable,B.1 and The inverse DTFT is
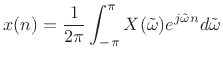
which can be derived in a manner analogous to the derivation of the inverse DFT (see Chapter 6).
Instead of operating on sampled signals of length ![]() (like the DFT),
the DTFT operates on sampled signals
(like the DFT),
the DTFT operates on sampled signals ![]() defined over all integers
defined over all integers
![]() . As a result, the DTFT frequencies form a
continuum. That is, the DTFT is a function of
continuous frequency
. As a result, the DTFT frequencies form a
continuum. That is, the DTFT is a function of
continuous frequency
![]() , while the DFT is a
function of discrete frequency
, while the DFT is a
function of discrete frequency ![]() ,
,
![]() . The DFT
frequencies
. The DFT
frequencies
![]() ,
,
![]() , are given by
the angles of
, are given by
the angles of ![]() points uniformly distributed along the unit circle
in the complex plane (see
Fig.6.1). Thus, as
points uniformly distributed along the unit circle
in the complex plane (see
Fig.6.1). Thus, as
![]() , a continuous frequency axis
must result in the limit along the unit circle in the
, a continuous frequency axis
must result in the limit along the unit circle in the ![]() plane. The
axis is still finite in length, however, because the time domain
remains sampled.
plane. The
axis is still finite in length, however, because the time domain
remains sampled.