![$\displaystyle 2\sum_{n=0}^{N-1} x(n) \cos\left[\frac{\pi k}{2N}(2n+1)\right],
\quad k=0,1,2,\ldots,N-1$](img1659.png) |
|||
![$\displaystyle 2\sum_{n=0}^{N-1} x(n) \cos\left[\omega_k\left(n+\frac{1}{2}\right)\right]
\protect$](img1660.png) |
(A.2) |
In image coding (such as MPEG and JPEG), and many audio coding
algorithms (MPEG), the discrete cosine transform (DCT) is used
because of its nearly optimal asymptotic theoretical
coding gain.A.9For 1D signals, one of several DCT definitions (the one called
DCT-II)A.10is given by
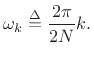
Note that
For real signals, the real part of the DFT is a kind of DCT:
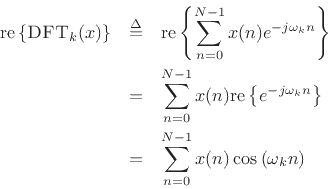
Thus, the real part of a double-length FFT is the same as the DCT
except for the half-sample phase shift in the sinusoidal basis
functions
![]() (and a scaling by 2 which is
unimportant).
(and a scaling by 2 which is
unimportant).
In practice, the DCT is normally implemented using the same basic efficiency techniques as in FFT algorithms. In Matlab and Octave (Octave-Forge), the functions dct and dct2 are available for the 1D and 2D cases, respectively.
Exercise: Using Euler's identity, expand the cosine in the DCT defined by Eq.(A.2) above into a sum of complex sinusoids, and show that the DCT can be rewritten as the sum of two phase-modulated DFTs:
where