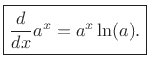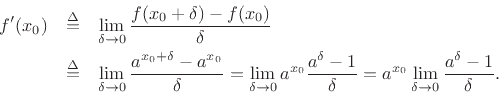
Let's apply the definition of differentiation and see what happens:
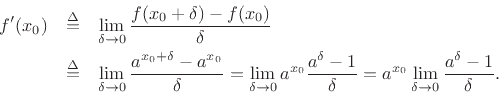
Since the limit of
![]() as
as
![]() is less than
1 for
is less than
1 for ![]() and greater than
and greater than ![]() for
for ![]() (as one can show via direct
calculations), and since
(as one can show via direct
calculations), and since
![]() is a continuous
function of
is a continuous
function of ![]() for
for ![]() , it follows that there exists a
positive real number we'll call
, it follows that there exists a
positive real number we'll call ![]() such that for
such that for ![]() we get
we get
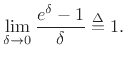
For
So far we have proved that the derivative of ![]() is
is ![]() .
What about
.
What about ![]() for other values of
for other values of ![]() ? The trick is to write it as
? The trick is to write it as
and use the chain rule,3.3 where
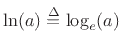 denotes
the log-base-
denotes
the log-base-
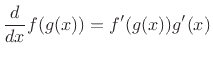
Evaluated at a particular point
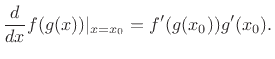
In this case,