When avoiding delay-line interpolation and accepting the angles given
by integer interspeaker delays, we should choose the sampling rate
![]() and speaker line-array spacing
and speaker line-array spacing ![]() so that the angles available
from each line array include the angles to the polygon vertices.
so that the angles available
from each line array include the angles to the polygon vertices.
For an ![]() -sided polygon, the two needed angles are
-sided polygon, the two needed angles are ![]() . The
set of all vertex angles is
. The
set of all vertex angles is
![]() ,
,
![]() ,
where
,
where ![]() is sound speed and
is sound speed and ![]() is the sampling interval. Thus,
we need some integer
is the sampling interval. Thus,
we need some integer ![]() to give
to give
![]() , or
, or
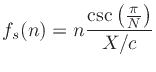
for some
In the four-quadrant case (four line arrays defining a square) with
speaker spacing ![]() in (example from §2.15 below), the
sampling rate wants to be a multiple of
in (example from §2.15 below), the
sampling rate wants to be a multiple of ![]() , and
, and ![]() kHz happens
to be
kHz happens
to be
![]() , so the 10th angle is very close to 45
degrees. For
, so the 10th angle is very close to 45
degrees. For ![]() polygon sides and four-inch speaker spacing, we
need
polygon sides and four-inch speaker spacing, we
need ![]() to be a multiple of
to be a multiple of ![]() , and it so happens that 44.1
kHz is close to five times that (
, and it so happens that 44.1
kHz is close to five times that (![]() ).
).
http://arxiv.org/abs/1911.07575.