Next |
Prev |
Up |
Top
|
Index |
JOS Index |
JOS Pubs |
JOS Home |
Search
Note that every real two-pole resonator can be broken up into a sum of
two complex one-pole resonators:
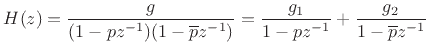 |
(B.7) |
where 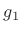 and
and 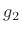 are constants (generally complex). In this
``parallel one-pole'' form, it can be seen that the peak gain is no
longer equal to the resonance gain, since each one-pole frequency
response is ``tilted'' near resonance by being summed with the
``skirt'' of the other one-pole resonator, as illustrated in
Fig.B.9. This interaction between the positive- and negative-frequency
poles is minimized by making the resonance sharper (
are constants (generally complex). In this
``parallel one-pole'' form, it can be seen that the peak gain is no
longer equal to the resonance gain, since each one-pole frequency
response is ``tilted'' near resonance by being summed with the
``skirt'' of the other one-pole resonator, as illustrated in
Fig.B.9. This interaction between the positive- and negative-frequency
poles is minimized by making the resonance sharper (
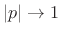 ),
and by separating the pole frequencies
),
and by separating the pole frequencies
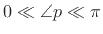 . The
greatest separation occurs when the resonance frequency is at
one-fourth the sampling rate (
. The
greatest separation occurs when the resonance frequency is at
one-fourth the sampling rate (
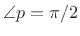 ). However,
low-frequency resonances, which are by far the most common in audio
work, suffer from significant overlapping of the positive- and
negative-frequency poles.
). However,
low-frequency resonances, which are by far the most common in audio
work, suffer from significant overlapping of the positive- and
negative-frequency poles.
To show Eq.(B.7) is always true, let's solve in general for 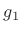 and
and 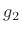 given
given 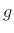 and
and 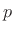 . Recombining the right-hand side
over a common denominator and equating numerators gives
. Recombining the right-hand side
over a common denominator and equating numerators gives
which implies
The solution is easily found to be
where we have assumed
im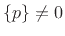 , as necessary to have a
resonator in the first place.
, as necessary to have a
resonator in the first place.
Breaking up the two-pole real resonator into a parallel sum of two
complex one-pole resonators is a simple example of a partial
fraction expansion (PFE) (discussed more fully in §6.8).
Note that the inverse z transform of a sum of one-pole transfer
functions can be easily written down by inspection. In particular,
the impulse response of the PFE of the two-pole resonator (see
Eq.(B.7)) is clearly
Since 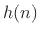 is real, we must have
is real, we must have
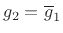 , as we found above
without assuming it. If
, as we found above
without assuming it. If
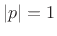 , then
, then 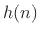 is a real sinusoid
created by the sum of two complex sinusoids spinning in opposite
directions on the unit circle.
is a real sinusoid
created by the sum of two complex sinusoids spinning in opposite
directions on the unit circle.
Next |
Prev |
Up |
Top
|
Index |
JOS Index |
JOS Pubs |
JOS Home |
Search
[How to cite this work] [Order a printed hardcopy] [Comment on this page via email]
![\includegraphics[width=\twidth ]{eps/tppfe}](img1433.png)
![]() and
and ![]() given
given ![]() and
and ![]() . Recombining the right-hand side
over a common denominator and equating numerators gives
. Recombining the right-hand side
over a common denominator and equating numerators gives
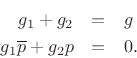
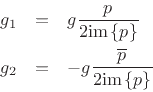
![]() , as necessary to have a
resonator in the first place.
, as necessary to have a
resonator in the first place.