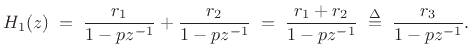
When poles are repeated, an interesting new phenomenon emerges. To see what's going on, let's consider two identical poles arranged in parallel and in series. In the parallel case, we have
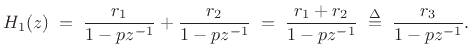
In the series case, we get
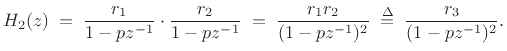
Thus, two one-pole filters in parallel are equivalent to a new one-pole filter7.8 (when the poles are identical), while the same two filters in series give a two-pole filter with a repeated pole. To accommodate both possibilities, the general partial fraction expansion must include the terms
for a pole