Next |
Prev |
Up |
Top
|
Index |
JOS Index |
JOS Pubs |
JOS Home |
Search
We want to show it is always possible to solve
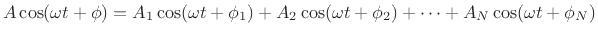 |
(A.2) |
for 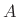 and
and  , given
, given
 for
for
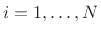 . For each
component sinusoid, we can write
. For each
component sinusoid, we can write
Applying this expansion to Eq.(A.2) yields
Equating coefficients gives
where  and
and 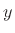 are known. We now have two equations in two
unknowns which are readily solved by (1) squaring and adding both
sides to eliminate
are known. We now have two equations in two
unknowns which are readily solved by (1) squaring and adding both
sides to eliminate  , and (2) forming a ratio of both sides of
Eq.(A.4) to eliminate
, and (2) forming a ratio of both sides of
Eq.(A.4) to eliminate 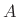 . This gives
. This gives
for any values of 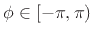 and
and  . Since
. Since
 , we have
, we have
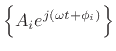 . To impose
. To impose 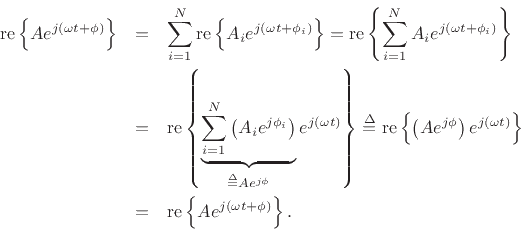 and
and
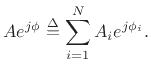 , a
four-quadrant arctangent
, a
four-quadrant arctangent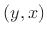 must be used, normally
written atan2(y,x) in computer languages.
must be used, normally
written atan2(y,x) in computer languages.
Next |
Prev |
Up |
Top
|
Index |
JOS Index |
JOS Pubs |
JOS Home |
Search
[How to cite this work] [Order a printed hardcopy] [Comment on this page via email]
![\begin{eqnarray*}
\left[A\cos(\phi)\right]\cos(\omega t)
&-&\left[A\sin(\phi)\right]\sin(\omega t)\\
&=& \left[\sum_{i=1}^N A_i\cos(\phi_i)\right]\cos(\omega t)
- \left[\sum_{i=1}^N A_i\sin(\phi_i)\right]\sin(\omega t).
\end{eqnarray*}](img1330.png)
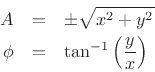
![]() and
and ![]() . Since
. Since
![]() , we have
, we have
![]() . To impose
. To impose ![]() and
and
![]() , a
four-quadrant arctangent
, a
four-quadrant arctangent![]() must be used, normally
written atan2(y,x) in computer languages.
must be used, normally
written atan2(y,x) in computer languages.