Next |
Prev |
Up |
Top
|
Index |
JOS Index |
JOS Pubs |
JOS Home |
Search
The heart of the preceding proof was the algebraic manipulation
The carrier term
 ``factors out'' of the sum.
Inside the sum, each sinusoid is represented by a complex constant
``factors out'' of the sum.
Inside the sum, each sinusoid is represented by a complex constant
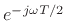 , known as the phasor associated with that
sinusoid.
, known as the phasor associated with that
sinusoid.
For an arbitrary sinusoid having amplitude 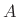 , phase
, phase  , and
radian frequency
, and
radian frequency 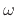 , we have
, we have
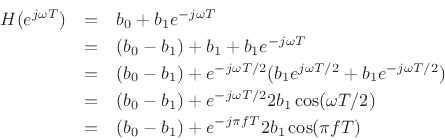
re
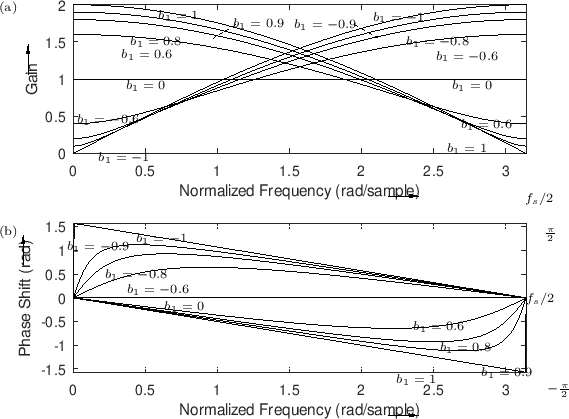
Thus, a sinusoid is determined by its frequency 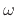 (which
specifies the carrier term) and its phasor
(which
specifies the carrier term) and its phasor
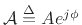 ,
a complex constant. Phasor analysis is discussed further in
[84].
,
a complex constant. Phasor analysis is discussed further in
[84].
Next |
Prev |
Up |
Top
|
Index |
JOS Index |
JOS Pubs |
JOS Home |
Search
[How to cite this work] [Order a printed hardcopy] [Comment on this page via email]
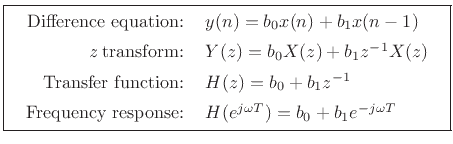
![]() , phase
, phase ![]() , and
radian frequency
, and
radian frequency ![]() , we have
, we have