One-Pole Transfer Functions

We can apply the same analysis to a one-pole transfer function. Let $p\in\mathbb{C}$ denote any real or complex number:

$$H(z) \eqsp \frac{1}{1-pz^{-1}} \eqsp 1 + pz^{-1}+ p^2z^{-2}+ p^3z^{-3} + \cdots$$

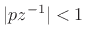
The convergence criterion is now $\vert pz^{-1}\vert<1$ , or $\vert z\vert>\vert p\vert$ . For the region of convergence to include the unit circle (our frequency axis), we must have $\vert p\vert<1$ , which is our usual stability criterion for a pole at $z=p$ . The inverse z transform is then the causal decaying sampled exponential

$$H(z) \;\longleftrightarrow\; h(n) = u(n)p^n$$

Now consider the rewritten case:

$$\begin{eqnarray*} \frac{1}{1-pz^{-1}} &=& \frac{-p^{-1}z}{1-p^{-1}z} \\ &=& -p^{-1}z\left[1 + p^{-1}z + p^{-2}z^2 + p^{-3}z^3 + \cdots\right]\\ &=& -\left[p^{-1}z + p^{-2}z^2 + p^{-3}z^3 + p^{-4}z^4 + \cdots\right]\\ &\leftrightarrow& - u(-n-1)p^n,\quad n\in\mathbb{Z} \end{eqnarray*}$$

where the inverse z transform is the inverse bilateral z transform. In this case, the convergence criterion is $\vert p^{-1}z\vert<1$ , or $\vert z\vert<\vert p\vert$ , and this region includes the unit circle when $\vert p\vert>1$ .

In summary, when the region-of-convergence of the z transform is assumed to include the unit circle of the $z$ plane, poles inside the unit circle correspond to stable, causal, decaying exponentials, while poles outside the unit circle correspond to anticausal exponentials that decay toward time $-\infty$ , and stop before time zero.

Figures 8.8(a) through 8.8(d) illustrate the two types of exponentials (causal and anticausal) that correspond to poles (inside and outside the unit circle) when the z transform region of convergence is defined to include the unit circle.

Figure: Causal exponential decay, pole at $p=0.9$ .

Figure: Corresponding impulse response, assuming the region of convergence includes the unit circle in the $z$ plane.

Figure: Anticausal exponential decay, pole at $p=1/0.9$ .

Figure: Corresponding impulse response, assuming the region of convergence includes the unit circle in the $z$ plane.