Next |
Prev |
Up |
Top
|
Index |
JOS Index |
JOS Pubs |
JOS Home |
Search
Linearity
The Laplace transform is a linear operator. To show this, let
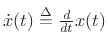 denote a linear combination of signals
denote a linear combination of signals  and
and 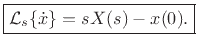 ,
,
where  and
and  are real or complex constants. Then we have
are real or complex constants. Then we have
Thus, linearity of the Laplace transform follows immediately from the
linearity of integration.
Next |
Prev |
Up |
Top
|
Index |
JOS Index |
JOS Pubs |
JOS Home |
Search
[How to cite this work] [Order a printed hardcopy] [Comment on this page via email]
![]() denote a linear combination of signals
denote a linear combination of signals ![]() and
and ![]() ,
,
![\begin{eqnarray*}
W(s) &\isdef & {\cal L}_s\{w\} \isdef {\cal L}_s\{\alpha x(t) + \beta y(t)\}\\
&\isdef & \int_0^\infty \left[\alpha x(t) + \beta y(t)\right] e^{-st} dt\\
&=& \alpha \int_0^\infty x(t) e^{-st} dt
+ \beta \int_0^\infty y(t) e^{-st} dt\\
&\isdef & \alpha X(s) + \beta Y(s).
\end{eqnarray*}](img1741.png)