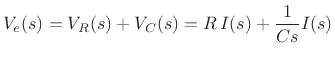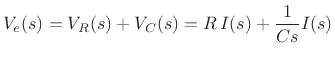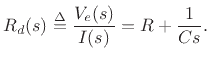Driving Point Impedance

Taking the Laplace transform of both sides of Eq.(E.1) gives

$$V_e(s) = V_R(s) + V_C(s) = R\, I(s) + \frac{1}{Cs} I(s)$$

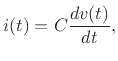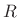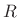where we made use of the fact that the impedance of a capacitor is $1/(Cs)$ , as derived above, and the impedance of a resistor $R$ is just $R$ (since impedance is defined as voltage over current for electrical systems, or force over velocity for mechanical systems). The driving point impedance of the whole RC filter is thus

$$R_d(s) \isdef \frac{V_e(s)}{I(s)} = R + \frac{1}{Cs}.$$

Alternatively, we could simply note that impedances always sum in series and write down this result directly.