Next |
Prev |
Up |
Top
|
Index |
JOS Index |
JOS Pubs |
JOS Home |
Search
Using Euler's identity to represent sinusoids, we have
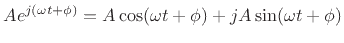 |
(2.9) |
when time  is continuous (see §A.1 for a list of notational
conventions), and when time is discrete,
is continuous (see §A.1 for a list of notational
conventions), and when time is discrete,
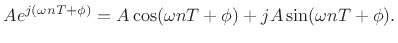 |
(2.10) |
Any function of the form
 or
or
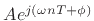 will henceforth be called a complex
sinusoid.2.3 We will
see that it is easier to manipulate both sine and
cosine simultaneously in this form than it is to deal with
either
sine or cosine separately. One may even take the
point of view that
will henceforth be called a complex
sinusoid.2.3 We will
see that it is easier to manipulate both sine and
cosine simultaneously in this form than it is to deal with
either
sine or cosine separately. One may even take the
point of view that
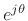 is simpler and more
fundamental than
is simpler and more
fundamental than
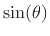 or
or
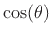 , as evidenced by
the following identities (which are immediate consequences of Euler's
identity,
Eq.(1.8)):
, as evidenced by
the following identities (which are immediate consequences of Euler's
identity,
Eq.(1.8)):
Thus, sine and cosine may each be regarded as a
combination of two complex sinusoids. Another reason for the success
of the complex sinusoid is that we will be concerned only with real
linear operations on signals. This means that 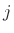 in Eq.(1.8)
will never be multiplied by
in Eq.(1.8)
will never be multiplied by 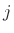 or raised to a power by a linear
filter with real coefficients. Therefore, the real and imaginary parts
of that equation are actually treated independently. Thus, we
can feed a complex sinusoid into a filter, and the real part of the
output will be the cosine response and the imaginary part of
the output will be the sine response. For the student new to
analysis using complex variables, natural questions at this point
include ``Why
or raised to a power by a linear
filter with real coefficients. Therefore, the real and imaginary parts
of that equation are actually treated independently. Thus, we
can feed a complex sinusoid into a filter, and the real part of the
output will be the cosine response and the imaginary part of
the output will be the sine response. For the student new to
analysis using complex variables, natural questions at this point
include ``Why  ?, Where did the imaginary exponent come from? Are
imaginary exponents legal?'' and so on. These questions are fully
answered in [84] and elsewhere [53,14].
Here, we will look only at some intuitive connections between complex
sinusoids and the more familiar real sinusoids.
?, Where did the imaginary exponent come from? Are
imaginary exponents legal?'' and so on. These questions are fully
answered in [84] and elsewhere [53,14].
Here, we will look only at some intuitive connections between complex
sinusoids and the more familiar real sinusoids.
Next |
Prev |
Up |
Top
|
Index |
JOS Index |
JOS Pubs |
JOS Home |
Search
[How to cite this work] [Order a printed hardcopy] [Comment on this page via email]
![]() or
or
![]() will henceforth be called a complex
sinusoid.2.3 We will
see that it is easier to manipulate both sine and
cosine simultaneously in this form than it is to deal with
either
sine or cosine separately. One may even take the
point of view that
will henceforth be called a complex
sinusoid.2.3 We will
see that it is easier to manipulate both sine and
cosine simultaneously in this form than it is to deal with
either
sine or cosine separately. One may even take the
point of view that
![]() is simpler and more
fundamental than
is simpler and more
fundamental than
![]() or
or
![]() , as evidenced by
the following identities (which are immediate consequences of Euler's
identity,
Eq.(1.8)):
, as evidenced by
the following identities (which are immediate consequences of Euler's
identity,
Eq.(1.8)):