Converting a digital filter to state-space form is easy because there are various ``canonical forms'' for state-space models which can be written by inspection given the strictly proper transfer-function coefficients.
The canonical forms useful for transfer-function to state-space conversion are controller canonical form (also called control or controllable canonical form) and observer canonical form (or observable canonical form) [28, p. 80], [37]. These names come from the field of control theory [28] which is concerned with designing feedback laws to control the dynamics of real-world physical systems. State-space models are used extensively in the control field to model physical systems.
The name ``controller canonical form'' reflects the fact that the
input signal can ``drive'' all modes (poles) of the system. In the
language of control theory, we may say that all of the system poles
are controllable from the input
![]() . In observer canonical form, all modes are guaranteed to be
observable. Controllability and observability of a state-space
model are discussed further in §G.7.3 below.
. In observer canonical form, all modes are guaranteed to be
observable. Controllability and observability of a state-space
model are discussed further in §G.7.3 below.
The following procedure converts any causal LTI digital filter into state-space form:
We now elaborate on these steps for the general case:
A causal filter contains a delay-free path if its impulse response
![]() is nonzero at time zero, i.e., if
is nonzero at time zero, i.e., if
![]() .G.5 In such cases, we must ``pull out'' the
delay-free path in order to implement it in parallel, setting
.G.5 In such cases, we must ``pull out'' the
delay-free path in order to implement it in parallel, setting
![]() in the state-space model.
in the state-space model.
In our example, one step of long division yields
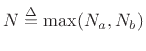 , with
, with
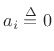 for
for 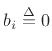 for
for
One might worry that choosing controller canonical form may result in
unobservable modes. However, this will not happen if ![]() and
and
![]() have no common factors. In other words, if there are no
pole-zero cancellations in the transfer function
have no common factors. In other words, if there are no
pole-zero cancellations in the transfer function
![]() ,
then either controller or observer canonical form will yield a
controllable and observable state-space model.
,
then either controller or observer canonical form will yield a
controllable and observable state-space model.
We now illustrate these steps using the example of Eq.(G.7):