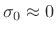The simplest case is a complex one-pole resonator having its
single pole at
![]() :
:

The maximum gain is readily found to be
Next, we need to find the 3dB-bandwidth. Without loss of generality,
we can set
![]() , since bandwidth is not changed for a complex
one-pole resonator by a vertical translation along the
, since bandwidth is not changed for a complex
one-pole resonator by a vertical translation along the ![]() axis. (Consider the graphical method for calculating amplitude
response from poles and zeros.) It is now easy to see that the
-3dB points of a ``dc resonance
axis. (Consider the graphical method for calculating amplitude
response from poles and zeros.) It is now easy to see that the
-3dB points of a ``dc resonance
![]() are at
are at
![]() :
:
![$\displaystyle \frac{\vert H[j(0\pm\sigma_0)]\vert^2}{\vert H(j0)\vert^2}
\eqsp \left.\left\vert\frac{1}{\pm j\sigma_0 - \sigma_0}\right\vert^2 \right/ \left\vert\frac{1}{ - \sigma_0}\right\vert^2
\eqsp \frac{\sigma_0^2}{\sigma_0^2+\sigma_0^2} = \frac{1}{2}.
$](img1894.png)
We have thus found that the ![]() of a complex one-pole resonator with pole at
of a complex one-pole resonator with pole at
![]() is given by
is given by