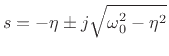Next |
Prev |
Up |
Top
|
Index |
JOS Index |
JOS Pubs |
JOS Home |
Search
From the quadratic formula, the two poles are located at
and there is a zero at  and another at
and another at 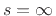 . If the
damping
. If the
damping  is sufficienly small so that
is sufficienly small so that
 , then
the poles form a complex-conjugate pair:
, then
the poles form a complex-conjugate pair:
Since
 , the poles are always in the left-half
plane, and hence the analog RLC filter is always stable. When the
damping is zero, the poles go to the
, the poles are always in the left-half
plane, and hence the analog RLC filter is always stable. When the
damping is zero, the poles go to the  axis:
axis:
Next |
Prev |
Up |
Top
|
Index |
JOS Index |
JOS Pubs |
JOS Home |
Search
[How to cite this work] [Order a printed hardcopy] [Comment on this page via email]