A peaking equalizer filter section provides a boost or cut in the vicinity of some center frequency. It may also be called a parametric equalizer section. The gain far away from the boost or cut is unity, so it is convenient to combine a number of such sections in series. Additionally, a high and/or low shelf (§B.4 above) are nice to include in series with one's peaking eq sections.
The analog transfer function for a peak filter is given by [103,5,6]
where
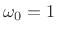
The transfer function can be written in the normalized form [103]
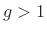
where
It is easy to show that both zeros and both poles are on the unit
circle in the left-half ![]() plane, and when
plane, and when ![]() (a ``cut''), the
zeros are closer to the
(a ``cut''), the
zeros are closer to the ![]() axis than the poles.
axis than the poles.
The bilinear transform (§I.3.1) can be used to convert the analog
peaking equalizer section to digital form. As derived in
§I.3.2, the mapping constant ![]() is best chosen as
is best chosen as
![]() , where
, where ![]() is the desired peak frequency
and
is the desired peak frequency
and ![]() is the sampling interval.
is the sampling interval.
Figure B.15 gives a matlab listing for a peaking equalizer section. Figure B.16 shows the resulting plot for the example ``boost(2,0.25,0.1).'' The frequency-response display utility myfreqz, listed in Fig.7.1, can be substituted for freqz (better for Octave).
function [B,A] = boost(g,fc,bw,fs); %BOOST - Design a digital boost filter at given gain g, % center frequency fc in Hz, % bandwidth bw in Hz (default = fs/10), and % sampling rate fs in Hz (default = 1). if nargin<4, fs = 1; end if nargin<3, bw = fs/10; end c = cot(pi*fc/fs); % bilinear transform constant cs = c^2; csp1 = cs+1; Bc=(bw/fs)*c; gBc=g*Bc; nrm = 1/(csp1 + Bc); % 1/(a0 before normalization) b0 = (csp1 + gBc)*nrm; b1 = 2*(1 - cs)*nrm; b2 = (csp1 - gBc)*nrm; a0 = 1; a1 = b1; a2 = (csp1 - Bc)*nrm; A = [a0 a1 a2]; B = [b0 b1 b2]; if nargout==0 figure(1); myfreqz(B,A); % /l/mll/myfreqz.m dstr=sprintf('boost(%0.2f,%0.2f,%0.2f,%0.2f)',g,fc,bw,fs); subplot(2,1,1); title(['Boost Frequency Response: ',... dstr],'fontsize',24); end |
![\includegraphics[width=\twidth]{eps/tboost}](img1509.png) |
A Faust implementation of the second-order peaking equalizer is available as the function peak_eq in filter.lib distributed with Faust (Appendix K).