Filter Order = Transfer Function Order

Recall that the order of a polynomial is defined as the highest power of the polynomial variable. For example, the order of the polynomial $p(x)=1+2x+3x^2$ is 2. From Eq.(8.1), we see that $M$ is the order of the transfer-function numerator polynomial in $z^{-1}$ . Similarly, $N$ is the order of the denominator polynomial in $z^{-1}$ .

A rational function is any ratio of polynomials. That is, $R(z)$ is a rational function if it can be written as

$$R(z)\eqsp \frac{P(z)}{Q(z)}$$

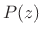
for finite-order polynomials $P(z)$ and $Q(z)$ . The order of a rational function is defined as the maximum of its numerator and denominator polynomial orders. As a result, we have the following simple rule:

$\parbox{0.9\textwidth}{\emph{The order of an LTI filter is the order of its transfer function.}}$

It turns out the transfer function can be viewed as a rational function of either $z^{-1}$ or $z$ without affecting order. Let $K=\max\{M,N\}$ denote the order of a general LTI filter with transfer function $H(z)$ expressible as in Eq.(8.1). Then multiplying $H(z)$ by $z^K/z^K$ gives a rational function of $z$ (as opposed to $z^{-1}$ ) that is also order $K$ when viewed as a ratio of polynomials in $z$ . Another way to reach this conclusion is to consider that replacing $z$ by $z^{-1}$ is a conformal map [57] that inverts the $z$ -plane with respect to the unit circle. Such a transformation clearly preserves the number of poles and zeros, provided poles and zeros at $z=\infty$ and $z=0$ are either both counted or both not counted.