Next |
Prev |
Up |
Top
|
Index |
JOS Index |
JOS Pubs |
JOS Home |
Search
The term sinusoid means a waveform of the type
 |
(A.1) |
Thus, a sinusoid may be defined as a cosine at amplitude 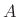 ,
frequency
,
frequency 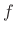 , and phase
, and phase 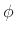 . (See [84] for a fuller
development and discussion.)
A sinusoid's phase
. (See [84] for a fuller
development and discussion.)
A sinusoid's phase 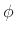 is in radian units. We may call
is in radian units. We may call
the instantaneous phase, as distinguished from the
phase offset 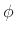 . Thus, the ``phase'' of a sinusoid
typically refers to its phase offset. The instantaneous
frequency of a sinusoid is defined as the derivative of the
instantaneous phase with respect to time (see [84] for more):
. Thus, the ``phase'' of a sinusoid
typically refers to its phase offset. The instantaneous
frequency of a sinusoid is defined as the derivative of the
instantaneous phase with respect to time (see [84] for more):
A discrete-time sinusoid is simply obtained from a continuous-time
sinusoid by replacing 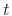 by
by 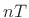 in Eq.(A.1):
in Eq.(A.1):
Next |
Prev |
Up |
Top
|
Index |
JOS Index |
JOS Pubs |
JOS Home |
Search
[How to cite this work] [Order a printed hardcopy] [Comment on this page via email]

![$\displaystyle f(t) \isdef \frac{d}{dt} \theta(t) = \frac{d}{dt} \left[\omega t + \phi\right] = \omega
$](img1307.png)