Yet another meaning for ![]() is [20, p. 326]
is [20, p. 326]
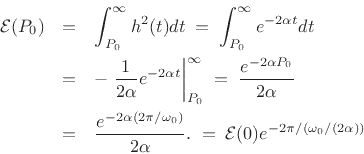
where the resonator is freely decaying (unexcited).
To analyze this, let's again consider a one-pole resonator as in §E.7.1. Then the impulse response is given by
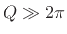
The total stored energy at time
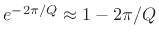
The energy dissipated in the first period
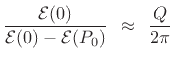
Assuming ![]() as before,
as before,
![]() so that
so that
Assuming further that
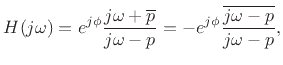
or
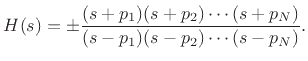
as claimed. Note that this rule of thumb requires