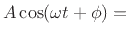Proof Using Complex Variables

To show by means of phasor analysis that Eq.(A.2) always has a solution, we can express each component sinusoid as

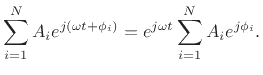
$$A_i\cos(\omega t + \phi_i) =$$   re$$\left\{A_i e^{j(\omega t + \phi_i)}\right\}$$

Equation (A.2) therefore becomes

$$\begin{eqnarray*} \mbox{re}\left\{A e^{j(\omega t + \phi)}\right\} &=& \sum_{i=1}^N \mbox{re}\left\{A_i e^{j(\omega t + \phi_i)}\right\} = \mbox{re}\left\{\sum_{i=1}^N A_i e^{j(\omega t + \phi_i)}\right\}\\ & = & \mbox{re}\left\{\underbrace{\sum_{i=1}^N \left(A_i e^{j\phi_i}\right)}_{\isdef Ae^{j\phi}} e^{j(\omega t)}\right\} \isdef \mbox{re}\left\{\left(A e^{j\phi}\right)e^{j(\omega t)}\right\}\\ &=& \mbox{re}\left\{A e^{j(\omega t+\phi)}\right\}. \end{eqnarray*}$$

Thus, equality holds when we define

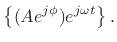$$A e^{j\phi} \isdef \sum_{i=1}^N A_i e^{j\phi_i}. \protect$$ (A.5)

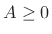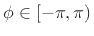Since $A e^{j\phi}$ is just the polar representation of a complex number, there is always some value of $A\geq 0$ and $\phi\in[-\pi,\pi)$ such that $A e^{j\phi}$ equals whatever complex number results on the right-hand side of Eq.(A.5).

As is often the case, we see that the use of Euler's identity and complex analysis gives a simplified algebraic proof which replaces a proof based on trigonometric identities.