Next |
Prev |
Up |
Top
|
Index |
JOS Index |
JOS Pubs |
JOS Home |
Search
A Musical Time-Varying Filter Example
Note, however, that a gain 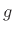 may vary with time independently
of
may vary with time independently
of 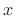 to yield a linear time-varying filter. In this case,
linearity may be demonstrated by verifying
to yield a linear time-varying filter. In this case,
linearity may be demonstrated by verifying
to show that both scaling and superposition hold. A simple example of a
linear time-varying filter is a tremolo function, which can be
written as a time-varying gain,
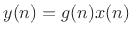 . For example,
. For example,
![$ g(n) = 1
+ \cos[2\pi (4)nT]$](img496.png) would give a maximally deep tremolo with 4 swells
per second.
would give a maximally deep tremolo with 4 swells
per second.
Next |
Prev |
Up |
Top
|
Index |
JOS Index |
JOS Pubs |
JOS Home |
Search
[How to cite this work] [Order a printed hardcopy] [Comment on this page via email]
![]() may vary with time independently
of
may vary with time independently
of ![]() to yield a linear time-varying filter. In this case,
linearity may be demonstrated by verifying
to yield a linear time-varying filter. In this case,
linearity may be demonstrated by verifying