As can be seen from the code listing, this implementation of
residuez simply calls residue, which was written to
carry out the partial fraction expansions of ![]() -plane
(continuous-time) transfer functions
-plane
(continuous-time) transfer functions ![]() :
:
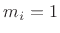
where ![]() is the ``quotient'' and
is the ``quotient'' and ![]() is the ``remainder'' in the PFE:
is the ``remainder'' in the PFE:
In the discrete-time case, we have the ![]() -plane transfer function
-plane transfer function
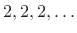
where ![]() .
.
We see that the ![]() -plane case formally does what we desire if we
treat
-plane case formally does what we desire if we
treat ![]() -plane polynomials as polynomials in
-plane polynomials as polynomials in ![]() instead of
instead of
![]() . From Eq.(J.2), we see that this requires reversing the
coefficient-order of B and A in the call to
residue. In the returned result, we obtain terms such as
. From Eq.(J.2), we see that this requires reversing the
coefficient-order of B and A in the call to
residue. In the returned result, we obtain terms such as

where the second form is simply the desired canonical form for
and the
Finally, the returned quotient polynomial must be flipped for the same reason that the input polynomials needed to be flipped (to convert from left-to-right descending powers of