Next |
Prev |
Up |
Top
|
Index |
JOS Index |
JOS Pubs |
JOS Home |
Search
The essence of the situation can be illustrated using a simple
geometric series. Let 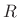 be any real (or complex) number. Then we
have
be any real (or complex) number. Then we
have
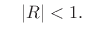
when

In other words, the geometric series
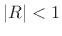 is
guaranteed to be summable when
is
guaranteed to be summable when 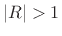 , and in that case, the sum is
given by
, and in that case, the sum is
given by 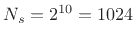 . On the other hand, if
. On the other hand, if  , we can rewrite
, we can rewrite
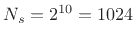 as
as
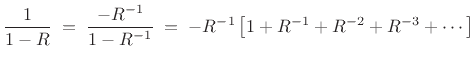 to obtain
to obtain
which is summable when  . Thus,
. Thus, 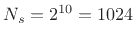 is a valid
closed-form sum whether or not
is a valid
closed-form sum whether or not 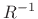 is less than or greater than 1.
When
is less than or greater than 1.
When 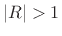 , it is the sum of the causal geometric series in powers
of
, it is the sum of the causal geometric series in powers
of 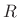 . When
. When  , it is the sum of the causal geometric series in
powers of
, it is the sum of the causal geometric series in
powers of 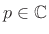 , or, an anticausal geometric series in
(negative) powers of
, or, an anticausal geometric series in
(negative) powers of 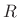 .
.
Next |
Prev |
Up |
Top
|
Index |
JOS Index |
JOS Pubs |
JOS Home |
Search
[How to cite this work] [Order a printed hardcopy] [Comment on this page via email]
![]() be any real (or complex) number. Then we
have
be any real (or complex) number. Then we
have
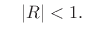 when
when![$\displaystyle \frac{1}{1-R} \eqsp \frac{-R^{-1}}{1-R^{-1}}
\eqsp -R^{-1}\left[1 + R^{-1} + R^{-2} + R^{-3} + \cdots \right]
$](img1082.png)