Choice of Output Signal and Initial Conditions

Recalling that ${\tilde x}= E\underline{{\tilde x}}$, the output signal from any diagonal state-space model is a linear combination of the modal signals. The two immediate outputs $x_1(n)$ and $x_2(n)$ in Fig.G.3 are given in terms of the modal signals ${\tilde x}_1(n) = \lambda_1^n{\tilde x}_1(0)$ and ${\tilde x}_2(n)= \lambda_2^n{\tilde x}_2(0)$ as

$$\begin{eqnarray*} y_1(n) &=& [1, 0] {\underline{x}}(n) = [1, 0] \left[\begin{arr... ...\lambda_1^n {\tilde x}_1(0) - \eta \lambda_2^n\,{\tilde x}_2(0). \end{eqnarray*}$$

The output signal from the first state variable $x_1(n)$ is

$$\begin{eqnarray*} y_1(n) &=& \lambda_1^n\,{\tilde x}_1(0) + \lambda_2^n\,{\tilde... ...{j\omega n T} {\tilde x}_1(0) + e^{-j\omega n T}{\tilde x}_2(0). \end{eqnarray*}$$

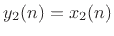
The initial condition ${\underline{x}}(0) = [1, 0]^T$ corresponds to modal initial state

$$\underline{{\tilde x}}(0) = E^{-1}\left[\begin{array}{c} 1 \\ [2p... ...nd{array}\right] = \left[\begin{array}{c} 1/2 \\ [2pt] 1/2 \end{array}\right].$$

For this initialization, the output $y_1$ from the first state variable $x_1$ is simply

$$y_1(n) = \frac{e^{j\omega n T} + e^{-j\omega n T}}{2} = \cos(\omega n T).$$

A similar derivation can be carried out to show that the output $y_2(n) = x_2(n)$ is proportional to $\sin(\omega nT)$, i.e., it is in phase quadrature with respect to $y_1(n)=x_1(n)$). Phase-quadrature outputs are often useful in practice, e.g., for generating complex sinusoids.