Next |
Prev |
Up |
Top
|
Index |
JOS Index |
JOS Pubs |
JOS Home |
Search
Fundamental Theorem of Algebra
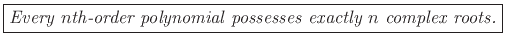
This is a very powerful algebraic tool.2.4 It says that given any polynomial
we can always rewrite it as
where the points 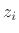 are the polynomial roots, and they may be real or
complex.
are the polynomial roots, and they may be real or
complex.
Next |
Prev |
Up |
Top
|
Index |
JOS Index |
JOS Pubs |
JOS Home |
Search
[How to cite this work] [Order a printed hardcopy] [Comment on this page via email]
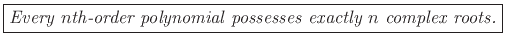


![]() are the polynomial roots, and they may be real or
complex.
are the polynomial roots, and they may be real or
complex.