Next |
Prev |
Up |
Top
|
JOS Index |
JOS Pubs |
JOS Home |
Search
From [2] I take the approximation of the curve in Fig. 2
as
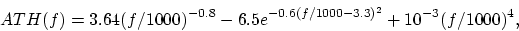 |
(6) |
where 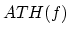 denotes the ATH in dB, and
denotes the ATH in dB, and 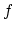 is the frequency in Hz. The
problem in digital audio coding,
is that one cannot know what absolute level the sound will be played
at. One common solution is to set the lowest point on the curve in
eq. 6 to be equal to the sound pressure level of a sine with
amplitude
is the frequency in Hz. The
problem in digital audio coding,
is that one cannot know what absolute level the sound will be played
at. One common solution is to set the lowest point on the curve in
eq. 6 to be equal to the sound pressure level of a sine with
amplitude 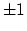 LSB.
In the coder, 16-bit samples with normalized amplitude to
LSB.
In the coder, 16-bit samples with normalized amplitude to
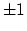 are used.
Thus, the smallest possible sine has amplitude
are used.
Thus, the smallest possible sine has amplitude 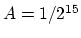 , and
has a power of
, and
has a power of
 .
The model used in the coder will thus be
.
The model used in the coder will thus be
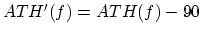 .
.
Next |
Prev |
Up |
Top
|
JOS Index |
JOS Pubs |
JOS Home |
Search
Download bosse.pdf