Critical Bandwidths

Much of what is done in Simultaneous Masking (see section 3.2) is based on the existence of critical bands. The hearing works much like a non-uniform filterbank, and the critical bands can be said to approximate the characteristics of those filters. Critical bands does not really have specific ``on'' and ``off'' frequencies, but rather width as a function of frequency - critical bandwidths.

The parameters for critical bandwidths can be derived in many ways [1], of which most give consistent results - which in some sense proves their presence. The critical bandwidths were first derived from the tone masking of white noise. Under the assumption that the tone was masked when the power of the noise in that critical band was equal to the about 1/4 of the power of the tone, critical bandwidth was determined to be

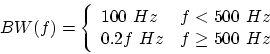$$BW(f) = \left \{ \begin{array}{lc} 100\ Hz & f < 500\ Hz \\ 0.2f\ Hz & f \ge 500\ Hz \\ \end{array} \right.$$ (7)

These bandwidths are used to form a critical band scale, rather similar to the logarithmic musical scale. Conversion between this bark frequency scale and Hz can be approximated via the function [2]

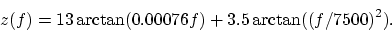$$z(f) = 13\arctan(0.00076f)+3.5\arctan((f/7500)^2).$$ (8)