Next |
Prev |
Up |
Top
|
JOS Index |
JOS Pubs |
JOS Home |
Search
The coefficients in a band are all quantized with the same step size 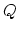 .
To store
.
To store 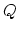 in the bit stream, it is indexed as
in the bit stream, it is indexed as
 |
(34) |
and thereafter Huffman encoded.
The 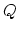 controls a nonuniform coefficient quantizer, with the following
characteristic.
controls a nonuniform coefficient quantizer, with the following
characteristic.
 |
(35) |
where a 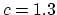 has proved to work well.
A nonuniform quantizer does not follow the masking threshold theories in
section 3.4, but works very well -- it is used in e.g MPEG-2
AAC [7].
has proved to work well.
A nonuniform quantizer does not follow the masking threshold theories in
section 3.4, but works very well -- it is used in e.g MPEG-2
AAC [7].
The coefficients of any orthogonal linear transform can be quantized as
described above, since
and so the quantizer makes no difference between the coefficients from the
different modes in section 4.2.2.
Next |
Prev |
Up |
Top
|
JOS Index |
JOS Pubs |
JOS Home |
Search
Download bosse.pdf
