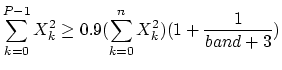Next |
Prev |
Up |
Top
|
JOS Index |
JOS Pubs |
JOS Home |
Search
Coefficient Clustering - Time Domain
At tonal parts of the signal, the frequency coefficients are highly
correlated in the time domain, since a tone corresponds to a stationary
peak in the frequency domain. This is exploited in the encoder by always
encoding four MDCT blocks at a time. To not get artifacts at transitions,
i.e when the masking threshold changes abruptly, two modes of
operation are introduced, one of which is chosen for each band:
- Transient mode. The four MDCT blocks are encoded individually,
and thus having an individual encoder step size per block and band. The MDCT
coefficients are quantized and encoded as described in section
4.2.4.
- Stationary mode. The four MDCT blocks are jointly coded, using only
one quantizer step size per band. The coefficients are transformed using a
fixed KLT (section 4.1.3), quantized and encoded. The KLT basis was
estimated from the tonal mono sequence strings.wav, which contains about
2000 frames.
The mode decision is done based on the mean of estimated variances of the
masking threshold over the four blocks for all frequencies in the band:
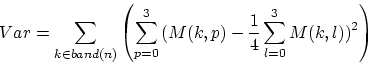 |
(31) |
If 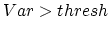 , then the Transient mode is used, otherwise Stationary mode.
The value
, then the Transient mode is used, otherwise Stationary mode.
The value
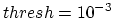 which is used in the coder, was found empirically.
which is used in the coder, was found empirically.
The Stationary mode tries to use the energy compaction property of the KLT
in the following fashion: Since the first few coefficients of the KLT
probably have
higher energy then the later ones, the transform can without greater loss
be performed with only a subset of the basis vectors 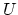 . Thus,
the
. Thus,
the 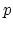 last coefficients from the KLT are never trasmitted.
Experiments has shown
that this works fine in the bands with many frequency bins, which leads to
the following heuristic for determining which coefficients to skip:
Use the
last coefficients from the KLT are never trasmitted.
Experiments has shown
that this works fine in the bands with many frequency bins, which leads to
the following heuristic for determining which coefficients to skip:
Use the 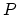 first coefficients, where
first coefficients, where 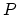 is chosen so that
is chosen so that
| |
|
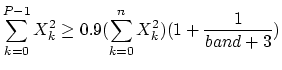 |
(32) |
| |
|
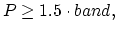 |
(33) |
where
![$band \in [0..23]$](img102.png) is the band number.
This heuristic ``cuts'' the transform when enough energy has been
included. More energy is required for lower bands, where tonal instruments,
such as strings, sound very bad without that restriction.
is the band number.
This heuristic ``cuts'' the transform when enough energy has been
included. More energy is required for lower bands, where tonal instruments,
such as strings, sound very bad without that restriction.
An experiment on audio clip music.wav gives the average
``coefficient ratio'' in table 4.2.1, where 1.0 corresponds to
sending all coefficients, and 0 to not sending any.
The effect of the weighting equations above is clearly visible in the
table. In e.g music.wav, the overall bitrate is 121 kbit/second without
the KLT and 106 with. It should be noted also that the KLT option without
the skipping of coefficients gives no bitrate savings. Thus, the
only gain I get from the KLT is that the quantization noise
from zeroed coefficients can be spread over the whole band.
Next |
Prev |
Up |
Top
|
JOS Index |
JOS Pubs |
JOS Home |
Search
Download bosse.pdf
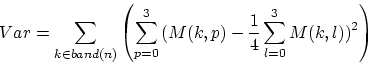
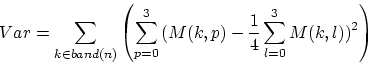
![]() . Thus,
the
. Thus,
the ![]() last coefficients from the KLT are never trasmitted.
Experiments has shown
that this works fine in the bands with many frequency bins, which leads to
the following heuristic for determining which coefficients to skip:
Use the
last coefficients from the KLT are never trasmitted.
Experiments has shown
that this works fine in the bands with many frequency bins, which leads to
the following heuristic for determining which coefficients to skip:
Use the ![]() first coefficients, where
first coefficients, where ![]() is chosen so that
is chosen so that