Next |
Prev |
Up |
Top
|
Index |
JOS Index |
JOS Pubs |
JOS Home |
Search
A partial differential equation (PDE) extends ODEs by adding
one or more independent variables (usually spatial variables). For
example, the wave equation for the ideal vibrating string adds one
spatial dimension 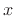 (along the axis of the string) and may be written as
follows:
(along the axis of the string) and may be written as
follows:
where 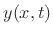 denotes the transverse displacement of the
string at position
denotes the transverse displacement of the
string at position 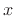 along the string and time
along the string and time 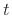 , and
, and
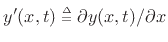 denotes the
partial derivative of
denotes the
partial derivative of 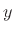 with respect to
with respect to
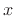 .2.7 The
physical parameters in this case are string tension
.2.7 The
physical parameters in this case are string tension 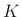 and string
mass-density
and string
mass-density 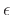 . This PDE is the starting point for both digital
waveguide models (Chapter 6) and finite difference schemes
(§C.2.1).
. This PDE is the starting point for both digital
waveguide models (Chapter 6) and finite difference schemes
(§C.2.1).
Next |
Prev |
Up |
Top
|
Index |
JOS Index |
JOS Pubs |
JOS Home |
Search
[How to cite this work] [Order a printed hardcopy] [Comment on this page via email]
![]() (along the axis of the string) and may be written as
follows:
(along the axis of the string) and may be written as
follows: