Kaiser (Kaiser-Bessel)

Kaiser discovered a very good approximation to prolate spheroidal wave functions using Bessel functions:

$$w_K(n) \mathrel{\stackrel{\Delta}{=}}\left\{ \begin{array}{ll} \frac{ I_0 \left( \beta \sqrt{ 1 - \left( \frac{n}{M/2}\right)^2} \right)}{ I_0(\beta) }, & -\frac{M-1}{2} \leq n \leq \frac{M-1}{2} \\ 0, & \mbox{elsewhere} \\ \end{array} \right.$$

$$w_K(n) \;\mathrel{\stackrel{\mathrm{\Delta}}{=}}\;w_R(n) \frac{ I_0 \left( \beta \sqrt{ 1 - \left( \frac{n}{M/2}\right)^2} \right)}{ I_0(\beta) }$$

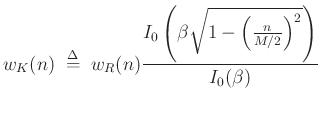
This is called the Kaiser (or Kaiser-Bessel) window.

The Fourier transform of the Kaiser window $w_K(t)$ (where $t$ is treated as continuous) is given by

$$\begin{eqnarray*} W(\omega) &=& \frac{M}{I_0(\beta)} \frac{\sinh\left(\sqrt{\beta^2 - \left(\frac{M \omega}{2}\right)^2}\right)} {\sqrt{ \beta^2 - \left(\frac{M\omega}{2}\right)^2}}\\ [10pt] &=& \frac{M}{I_0(\beta)} \frac{\sin\left(\sqrt{\left(\frac{M \omega}{2}\right)^2-\beta^2}\right)} {\sqrt{\left(\frac{M\omega}{2}\right)^2 - \beta^2}} \end{eqnarray*}$$

where $I_0$ is the zero-order modified Bessel function of the first kind.