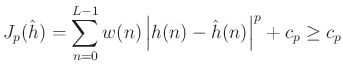Optimal (but Poor) Least-Squares Impulse Response Design

Let

• $h(n)$ = ideal filter impulse response.
• ${\hat h}(n)$ = length $L$ causal FIR filter (to be designed).

Sum of squared errors:

$$J_2({\hat h}) \isdef \sum_{n=-\infty}^\infty\left\vert h(n)-{\hat h}(n)\right\vert^2 = \sum_{n=0}^{L-1}\left\vert h(n)-{\hat h}(n)\right\vert^2 + c_2$$

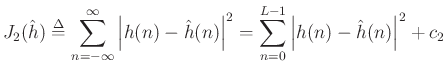
where 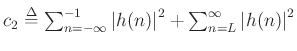$c_2\isdef \sum_{n=-\infty}^{-1}\left\vert h(n)\right\vert^2 + \sum_{n=L}^\infty\left\vert h(n)\right\vert^2$ does not depend on ${\hat h}$ . Note that $J_2({\hat h})\geq c_2$ .

Result: The error is minimized (in the least-squares sense) by simply matching the first $L$ terms in the desired impulse response.

Optimal least-squares FIR filter:

$${\hat h}(n) \isdef \left\{\begin{array}{ll} h(n), & 0\leq n \leq L-1 \\ [5pt] 0, & \hbox{otherwise} \\ \end{array} \right.$$

Also optimal under any $\ensuremath{L_p}$ norm with any error weighting:

$$J_p({\hat h}) = \sum_{n=0}^{L-1}w(n)\left\vert h(n)-{\hat h}(n)\right\vert^p + c_p \geq c_p$$