Matlab hilbert() function

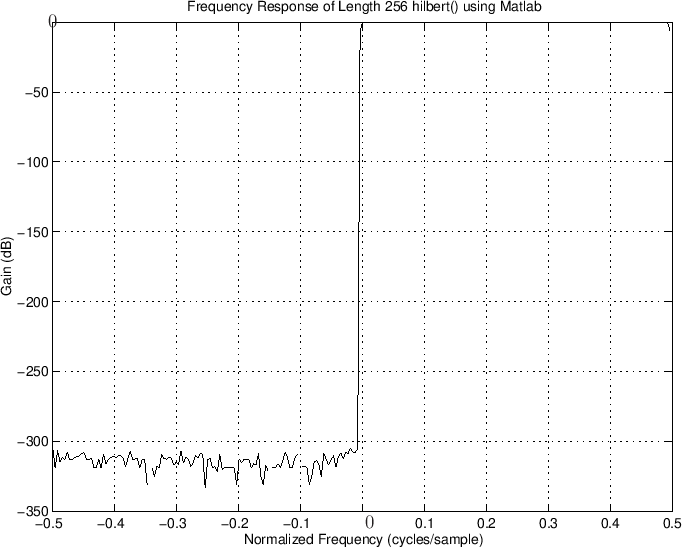
The Matlab Hilbert function returns an analytic signal given its real part.

Nh = M-2; % This looks best
delta = [1,zeros(1,Nh)]; % zero-centered impulse
hh = hilbert(delta); % zeros negative-freq FFT bins
Hh = fft(hh); % FIR frequency response

Looks pretty good, but let's zero-pad the impulse response to interpolate the frequency response:

hhzp = [hh(Lh/2+1:Lh), zeros(1,N-Lh), hh(1:Lh/2)];
Hhzp = fft(hhzp); % Frequency response

Problems:

• Transition bandwidth only 2 bins wide

• Massive time aliasing

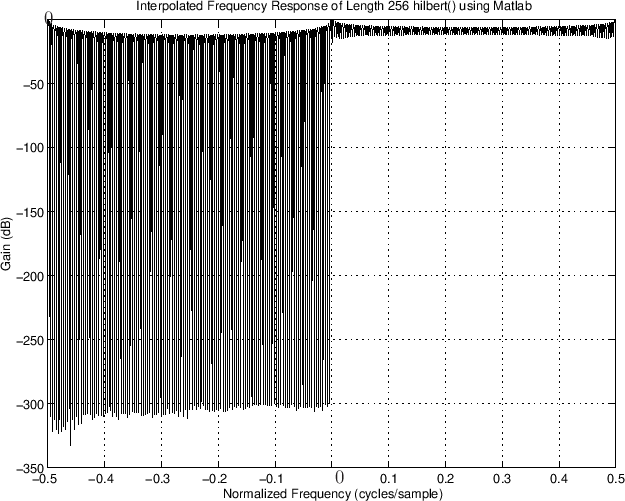
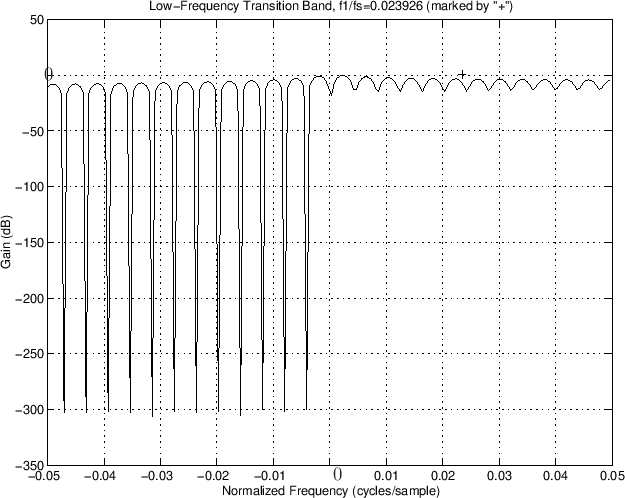
• Only correct for periodic signals with period exactly equal to filter length Nh. In this case, time aliasing is equivalent to overlap-add from adjacent periods.

In general, any real signal given to hilbert() must be interpreted as precisely one period of a periodic signal.