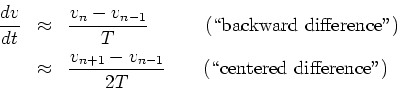Next |
Prev |
Top
|
JOS Index |
JOS Pubs |
JOS Home |
Search
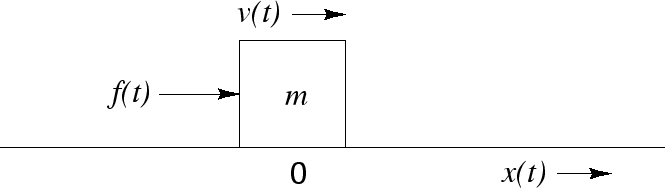
Consider the simple differential equation relating velocity and force
for an ideal mass:
Finite Difference Approximation:
E.g.,
(FDA for a force-driven mass)
Subsections
Next |
Prev |
Top
|
JOS Index |
JOS Pubs |
JOS Home |
Search
Download SMAC03S.pdf
Download SMAC03S_2up.pdf