Next |
Prev |
Up |
Top
|
JOS Index |
JOS Pubs |
JOS Home |
Search
- Models of damping in practical physical systems are rarely
completely independent of frequency, like the ideal dashpot
- Thanks to the Laplace transform (or Fourier
transform), the concept of impedance easily extends to masses and
springs as well
- We need only allow impedances to be frequency-dependent
- For example, the Laplace transform of Newton's
 yields, by
the differentiation theorem,
yields, by
the differentiation theorem,
where
-
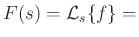 Laplace transform of
Laplace transform of 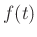 (initial conditions assumed zero)
(initial conditions assumed zero)
- Impedance of a point-mass is
- Specializing the Laplace transform to the Fourier transform by setting
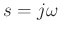 gives
gives
- Impedance of a spring with spring-constant
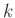 is
is
Next |
Prev |
Up |
Top
|
JOS Index |
JOS Pubs |
JOS Home |
Search
Download ReviewPM.pdf
Download ReviewPM_2up.pdf
Download ReviewPM_4up.pdf
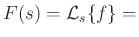 Laplace transform of
Laplace transform of 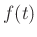 (initial conditions assumed zero)
(initial conditions assumed zero)
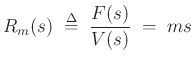
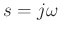 gives
gives
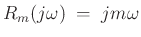
 is
is
![\begin{eqnarray*}
R_k(s) &=& \frac{k}{s}\\ [5pt]
R_k(j\omega) &=& \frac{k}{j\omega}
\end{eqnarray*}](img145.png)
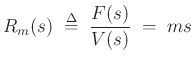
![\begin{eqnarray*}
R_k(s) &=& \frac{k}{s}\\ [5pt]
R_k(j\omega) &=& \frac{k}{j\omega}
\end{eqnarray*}](img145.png)