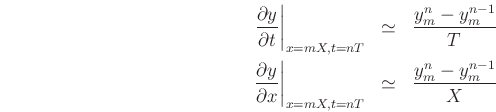
The simplest (and traditional) way of discretizing the 1D wave equation is by replacing first derivatives by first-order differences
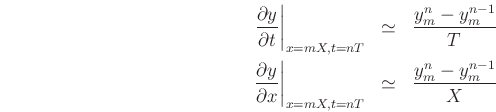
and second derivatives by second-order differences
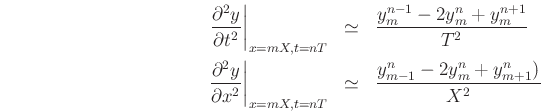
and so on, where
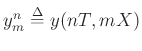 are the grid
variables. Note that we have uniformly sampled the time-space
plane, with timestep
are the grid
variables. Note that we have uniformly sampled the time-space
plane, with timestep ![]() (the temporal sampling interval)
and space step
(the temporal sampling interval)
and space step ![]() (the spatial sampling interval).
(the spatial sampling interval).