![\begin{eqnarray*}
x(n) &\mathrel{\stackrel{\Delta}{=}}& \frac{1}{N} \sum_{k=0}^{N-1}e^{j\omega_kn} \eqsp
\left\{
\begin{array}{ll}
1 & n=0 \quad (\hbox{\sc mod}\ N) \\
0 & \mbox{elsewhere} \\
\end{array} \right. \\ [10pt]
&=& \hbox{\sc IDFT}_{N,n}(1 \cdots 1) \;=\; \delta(n) + \delta(n-N) + \delta(n+N) + \cdots
\end{eqnarray*}](img145.png)
First consider the summation of N complex exponentials:
![\begin{eqnarray*}
x(n) &\mathrel{\stackrel{\Delta}{=}}& \frac{1}{N} \sum_{k=0}^{N-1}e^{j\omega_kn} \eqsp
\left\{
\begin{array}{ll}
1 & n=0 \quad (\hbox{\sc mod}\ N) \\
0 & \mbox{elsewhere} \\
\end{array} \right. \\ [10pt]
&=& \hbox{\sc IDFT}_{N,n}(1 \cdots 1) \;=\; \delta(n) + \delta(n-N) + \delta(n+N) + \cdots
\end{eqnarray*}](img145.png)
where
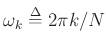 .
.
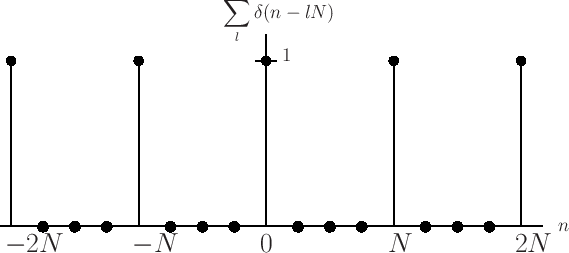
Setting ![]() (the FFT hop size) gives
(the FFT hop size) gives
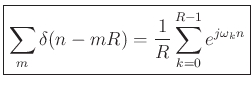
where
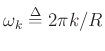 (harmonics of the frame rate).
(harmonics of the frame rate).
Let us now consider these equivalent signals as inputs to an LTI
system, with an impulse response given by ![]() , and frequency response
equal to
, and frequency response
equal to ![]() .
.
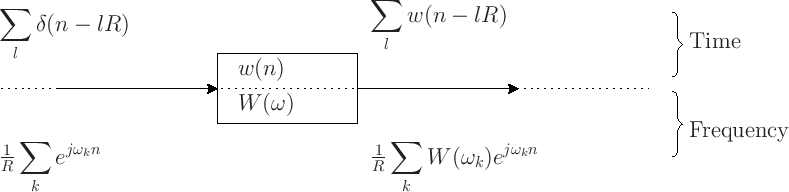
Looking across the top of the above figure, for the case of input signal
![]() we have:
we have:
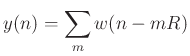
and looking across the bottom of the above figure, for the case of input
signal
![]() , we have:
, we have:
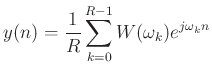
Since the inputs were equal, the corresponding outputs must be equal too. This derives the Poisson Summation Formula: