Consider breaking the input signal ![]() , into frames using a finite,
zero-centered, length
, into frames using a finite,
zero-centered, length ![]() (odd) window. Let
(odd) window. Let ![]() denote the
denote the ![]() frame.
frame.
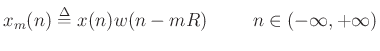
or

where
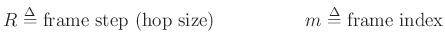
The hop size is the number of samples between adjacent frames. Specifically, it is the number of samples by which we advance each succesive window.
For fast convolution only, choose