Periodogram Normalization

Periodogram Definition:

$$P_{x,M}(\omega) \;\mathrel{\stackrel{\mathrm{\Delta}}{=}}\; \frac{1}{M} \left\vert\hbox{\sc DTFT}(x_w)\right\vert^2$$

To relate to power spectral density (PSD), check the dc sample:

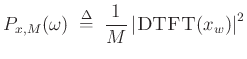
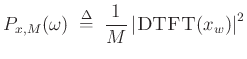
$$\begin{eqnarray*} {\cal E}\{P_{x,M}(0)\} &=& \frac{1}{M} {\cal E}\left\{\left(\sum_{n=-\infty}^{\infty}w_R(n)x(n)\right)^2\right\}\\ [5pt] &=& \frac{1}{M} \sum_{n=0}^{M-1}{\cal E}\{x^2(n)\}\\ [5pt] &=& \sigma_x^2 \end{eqnarray*}$$

• To be true to its name, the integral (sum) over the Power Spectral Density (PSD) should equal the total signal variance $\sigma_x^2 = {\cal E}\{x^2(n)\}$
• For white noise, which has PSD $S_x(\omega) = \sigma_x^2$ , the periodogram can be divided by $M$ again to give a spectral density estimate in variance per bin