Next |
Prev |
Up |
Top
|
JOS Index |
JOS Pubs |
JOS Home |
Search
As an example, when 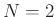 ,
,
![$ y[n] = x[2n]$](img46.png) , and
, and
(since
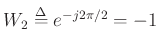 )
)
Next |
Prev |
Up |
Top
|
JOS Index |
JOS Pubs |
JOS Home |
Search
Download JFB.pdf
Download JFB_2up.pdf
Download JFB_4up.pdf
[Comment on this page via email]
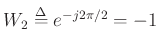 )
)
![]() ,
,
![]() , and
, and
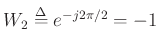 )
)
![\begin{eqnarray*}
Y(z) &=& \frac{1}{2}\left[X\left(W^0_2 z^{1/2}\right) + X\left(W^1_2 z^{1/2}\right)\right] \\ [0.1in]
&=& \frac{1}{2}\left[X\left(e^{-j2\pi 0/2} z^{1/2}\right) + X\left(e^{-j2\pi 1/2}z^{1/2}\right)\right] \\ [0.1in]
&=& \frac{1}{2}\left[X\left(z^{1/2}\right) + X\left(-z^{1/2}\right)\right] \\ [0.1in]
&=& \frac{1}{2}\left[\hbox{\sc Stretch}_2(X) + \hbox{\sc Stretch}_2\left(\hbox{\sc Shift}_\pi(X)\right)\right]
\end{eqnarray*}](img48.png)