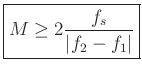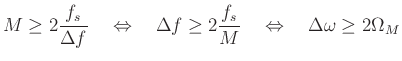A conservative requirement for resolving 2 sinusoids (in noisy
conditions) with a spacing of ![]() Hz is to choose a window
length
Hz is to choose a window
length ![]() long enough so that their main lobes are clearly discernible.
For example, we may require that their main lobes meet at the first
zero crossings.
long enough so that their main lobes are clearly discernible.
For example, we may require that their main lobes meet at the first
zero crossings.
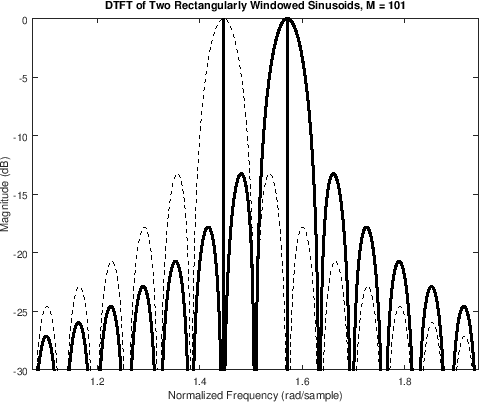
To obtain the separation shown above, we must have
![]() , where
, where
![]() is the main lobe width in Hz, and
is the main lobe width in Hz, and ![]() is the sinusoidal
frequency separation in Hz.
is the sinusoidal
frequency separation in Hz.
For the rectangular window, ![]() can be expressed as
can be expressed as
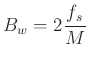
Hence we need:
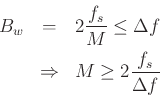
or