Ideal Bandlimited (Sinc) Interpolation

Ideal interpolation for digital audio is bandlimited interpolation, i.e., samples are uniquely interpolated based on the assumption of zero spectral energy for $\left\vert f\right\vert\geq f_s/2$ .

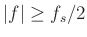Ideal bandlimited interpolation is sinc interpolation:

$$y(t) = (y\ast h_s)(t) = \sum_{n=-\infty}^\infty y(nT) h_s(t-nT)$$

where

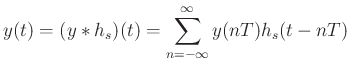
$$\begin{eqnarray*} h_s(t) &\mathrel{\stackrel{\mathrm{\Delta}}{=}}& \mbox{sinc}(f_st) \;\mathrel{\stackrel{\mathrm{\Delta}}{=}}\;\mbox{sinc}\left(\frac{t}{T}\right) \\ [10pt] \mbox{sinc}(x) &\mathrel{\stackrel{\mathrm{\Delta}}{=}}& \frac{\sin(\pi x)}{\pi x} \qquad\mbox{(sinc function)} \end{eqnarray*}$$

(Proof: sampling theorem)