Deriving Linear Interpolation from Taylor Series

Truncate a Taylor series expansion to first order and plug in a first-order derivative approximation:

$$\begin{eqnarray*} y(n+\alpha) &=& y(n) + \alpha\,\dot{y}(n) + \alpha^2\,\frac{\ddot{y}(n)}{2!} + \alpha^3\,\frac{\dddot{y}(n)}{3!} + \cdots\\ [10pt] &\approx& y(n) + \alpha\,\dot{y}(n) \end{eqnarray*}$$

$$\begin{eqnarray*} \Rightarrow\quad{\hat y}(n+\alpha) &\mathrel{\stackrel{\mathrm{\Delta}}{=}}& y(n) + \alpha\,\frac{y(n+1)-y(n)}{1}\\ [10pt] &=& \alpha\,y(n+1) + (1-\alpha)\,y(n) \end{eqnarray*}$$

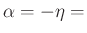where $\alpha=-\eta =$ fractional advance desired
(interpolation time between samples 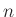$n$ and $n+1$ )

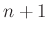• Same approach can be used to define higher-order interpolation filters using various choices of higher-order derivative approximations

• Recall the many finite-difference schemes we have