Uniform Distribution
Among probability distributions ![]() which are nonzero over a
finite range of values
which are nonzero over a
finite range of values ![]() , the maximum entropy
distribution is the uniform distribution.
, the maximum entropy
distribution is the uniform distribution.
To show this, we must maximize the entropy,
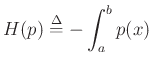 lg
lgwith respect to

Using the method of Lagrange multipliers for optimization in the presence of constraints, we may form the objective function
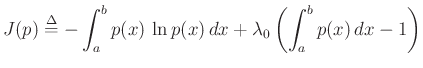
and differentiate with respect to
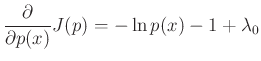
Setting this to zero and solving for
(Setting the partial derivative with respect to
Choosing ![]() to satisfy the constraint gives
to satisfy the constraint gives
![]() , yielding
, yielding
![$\displaystyle p(x) = \left\{\begin{array}{ll}
\frac{1}{b-a}, & a\leq x \leq b \\ [5pt]
0, & \hbox{otherwise} \\
\end{array} \right.
$](img129.png)
That this solution is a maximum rather than a minimum or inflection point can be verified by ensuring the sign of the second partial derivative is negative for all
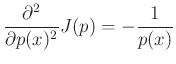
Since the solution spontaneously satisfied
Exponential Distribution
Among probability distributions ![]() which are nonzero over a
semi-infinite range of values
which are nonzero over a
semi-infinite range of values
![]() and having a finite
mean
and having a finite
mean ![]() , the exponential distribution has maximum entropy.
, the exponential distribution has maximum entropy.
To the previous case, we add the new constraint
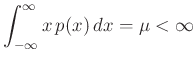
resulting in the objective function
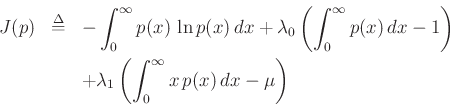
Now the partials with respect to ![]() are
are
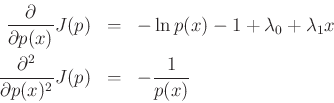
and ![]() is of the form
is of the form
![]() . The
unit-area and finite-mean constraints result in
. The
unit-area and finite-mean constraints result in
![]() and
and
![]() , yielding
, yielding
![$\displaystyle p(x) = \left\{\begin{array}{ll}
\frac{1}{\mu} e^{-x/\mu}, & x\geq 0 \\ [5pt]
0, & \hbox{otherwise} \\
\end{array} \right.
$](img139.png)
The Gaussian distribution has maximum entropy relative to all
probability distributions covering the entire real line
![]() but having a finite mean
but having a finite mean ![]() and finite
variance
and finite
variance ![]() .
.
Proceeding as before, we obtain the objective function
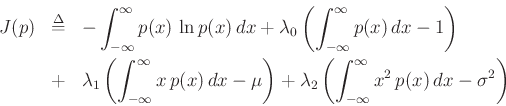
and partial derivatives
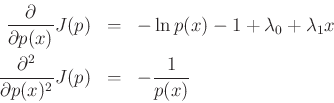
leading to

For more on entropy and maximum-entropy distributions, see (Cover and Thomas 1991).