We know from the foregoing that the denominator of the cone reflectance has
at least one root at ![]() . We now investigate the ``dc behavior''
more thoroughly.
. We now investigate the ``dc behavior''
more thoroughly.
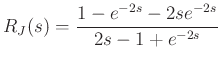
We already discovered a root at
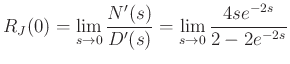
and once again the limit is an indeterminate
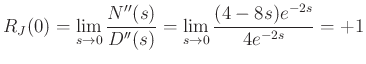
Thus, two poles and zeros cancel at dc, and the dc reflectance is
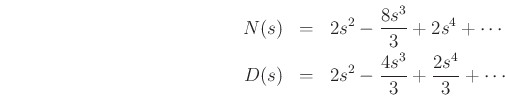
Both series begin with the term ![]() which means both the numerator
and denominator have two roots at
which means both the numerator
and denominator have two roots at ![]() . Hence, again the conclusion
is two pole-zero cancellations at dc.
. Hence, again the conclusion
is two pole-zero cancellations at dc.
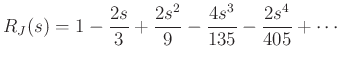
which approaches