




Next: Energetic Identities, Manipulations and
Up: Grid Functions and Difference
Previous: Matrix Interpretation of Difference
Contents
Index
Inner Products and Identities
Energy analysis of PDE systems is based, usually, around the definition of various types of spatial inner products. A very useful choice in the continuous case is the 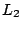 inner product, In 1D, it, along with the accompanying norm, is defined as
inner product, In 1D, it, along with the accompanying norm, is defined as
![$\displaystyle \langle f,g \rangle_{[a,b]} = \int_{a}^{b}fgdx\qquad \Vert f\Vert _{[a,b]}=\langle f,g\rangle_{[a,b]}$](img350.png) |
(5.7) |
for functions 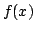 and
and 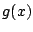 defined over the interval
defined over the interval ![$ x\in[a,b]$](img353.png) . For time-dependent problems such as those encountered in this book, such an inner product when applied to two functions
. For time-dependent problems such as those encountered in this book, such an inner product when applied to two functions 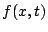 and
and 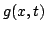 will itself be a function of time, i.e.,
will itself be a function of time, i.e.,
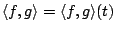 . The Cauchy-Schwartz and triangle inequalities follow from the above definition as
. The Cauchy-Schwartz and triangle inequalities follow from the above definition as
![$\displaystyle \begin{eqnarray}\vert\langle f,g\rangle_{[a,b]}\vert&\leq& \Vert ...
...[r,s]}&\leq& \Vert f^{n}\Vert _{[r,s]}+\Vert g^{n}\Vert _{[r,s]} \end{eqnarray}$](img357.png) |
(5.8a) |
As one might gather, an essential step towards energy-based analysis of finite difference schemes for distributed problems is the introduction of a spatial inner product between two grid functions, which is analogous to the above continuous definition. There are clearly many ways of doing this, but the simplest is the following: one simple 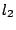 spatial inner product of two one-dimensional grid functions,
spatial inner product of two one-dimensional grid functions, 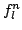 and
and 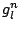 , over the interval
, over the interval ![$ l\in[r,s]$](img361.png) , may be defined as
, may be defined as
![$\displaystyle \langle f^{n},g^{n}\rangle_{[r,s]} =\sum_{l=r}^{s}hf_{l}^{n}g_{l}^{n}$](img362.png) |
(5.9) |
The inner product is a scalar time series, dependent on 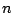 . An
. An 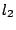 norm follows as
norm follows as
![$\displaystyle \Vert f^{n}\Vert _{[r,s]}=\sqrt{\langle f^{n},f^{n}\rangle_{[r,s]}}\geq 0$](img363.png) |
(5.10) |
The Cauchy-Schwartz and triangle inequalities follow immediately as
![$\displaystyle \begin{eqnarray}\vert\langle f^{n},g^{n}\rangle_{[r,s]}\vert&\leq...
...[r,s]}&\leq& \Vert f^{n}\Vert _{[r,s]}+\Vert g^{n}\Vert _{[r,s]} \end{eqnarray}$](img364.png) |
(5.11a) |
It is sometimes useful to define other types of inner products, which vary slightly from the above definition in (5.9); these usually are distinct at the endpoints of the spatial interval over which the inner product is defined. One of particular interest is given by
![$\displaystyle \langle f^{n},g^{n}\rangle_{[r,s]}' =\sum_{l=r+1}^{s-1}hf_{l}^{n}g_{l}^{n}+\frac{h}{2}f_{r}^{n}g_{r}^{n}+\frac{h}{2}f_{s}^{n}g_{s}^{n}$](img365.png) |
(5.12) |
A norm can again be defined in terms of this inner product, as per (5.10), and the Cauchy-Schwartz and triangle inequalities, from (5.11) above also hold. As might be imagined, the use of such an inner product leads to variations in the way boundary numerical boundary conditions are posed. Some more comments on this appear in the next section.





Next: Energetic Identities, Manipulations and
Up: Grid Functions and Difference
Previous: Matrix Interpretation of Difference
Contents
Index
Stefan Bilbao
2006-11-15
![]() inner product, In 1D, it, along with the accompanying norm, is defined as
inner product, In 1D, it, along with the accompanying norm, is defined as
![$\displaystyle \langle f,g \rangle_{[a,b]} = \int_{a}^{b}fgdx\qquad \Vert f\Vert _{[a,b]}=\langle f,g\rangle_{[a,b]}$](img350.png)
![]() spatial inner product of two one-dimensional grid functions,
spatial inner product of two one-dimensional grid functions, ![]() and
and ![]() , over the interval
, over the interval ![]() , may be defined as
, may be defined as