Using the Energy Decay Relief (EDR)

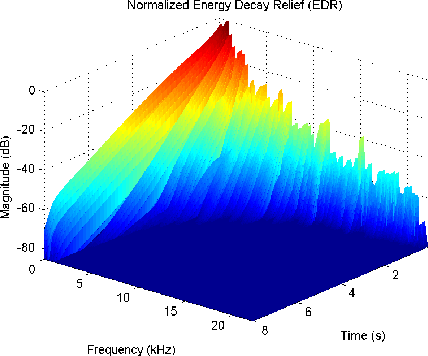
Compute the Energy Decay Relief (EDR) [1] of the original signal. Here we use Matlab's Signal Processing Toolkit. The function spectrogram computes the Short-Time Fourier Transform (STFT) of the signal. From the STFT, we compute the EDR. Figure 2 and Fig.3 show EDRs for the recorded note.

Figure 2: EDR of the signal truncated at -85 dB

Figure 3: EDR of the signal without truncation

We've provided the following code segments to demonstrate usage of the Signal Processing Toolbox in Matlab, as well as three-dimensional plotting.

frameSizeMS = 30; % minimum frame length, in ms
overlap = 0.75; % fraction of frame overlapping
windowType = 'hann'; % type of windowing used for each frame

[signal,fs,bits] = wavread(fileName);

% calculate STFT frames
minFrameLen = fs*frameSizeMS/1000; 
frameLenPow = nextpow2(minFrameLen);
frameLen = 2^frameLenPow; % frame length = fft size
eval(['frameWindow = ' windowType '(frameLen);']);
[B,F,T] = spectrogram(signal,frameWindow,overlap*frameLen,2*STFT_Npt,fs);

[nBins,nFrames] = size(B);

B_energy = B.*conj(B);
B_EDR = zeros(nBins,nFrames);
for i=1:nBins
    B_EDR(i,:) = fliplr(cumsum(fliplr(B_energy(i,:))));
end
B_EDRdb = 10*log10(abs(B_EDR));

% normalize EDR to 0 dB and truncate the plot below a given dB threshold
offset = max(max(B_EDRdb));
B_EDRdbN = B_EDRdb-offset;

B_EDRdbN_trunc = B_EDRdbN;
for i=1:nFrames
  I = find(B_EDRdbN(:,i) < minPlotDB);
  if (I)
    B_EDRdbN_trunc(I,i) = minPlotDB;
  end
end

figure(gcf);clf;
mesh(T,F/1000,B_EDRdbN_trunc);
view(130,30);
title('Normalized Energy Decay Relief (EDR)');
xlabel('Time (s)');ylabel('Frequency (kHz)');zlabel('Magnitude (dB)');
axis tight;zoom on;