Part 3: Fundamental Frequency

Now that we've looked at what the waveform looks like on a scale of seconds, let's turn to what the waveform looks like on a scale of milliseconds. The waveform window shows a 200ms sample of the waveform. Pluck the string and take a look at what the wave looks like.

1. The waveform window can be paused to take a snapshot by pressing the ``pause'' button. It can be restarted with the ``begin'' button. Pluck the string and pause the waveform shortly thereafter. An example waveform is shown in Figure 5.

   Figure 5: Screen-shot showing lower portion of patch 1-1.

   

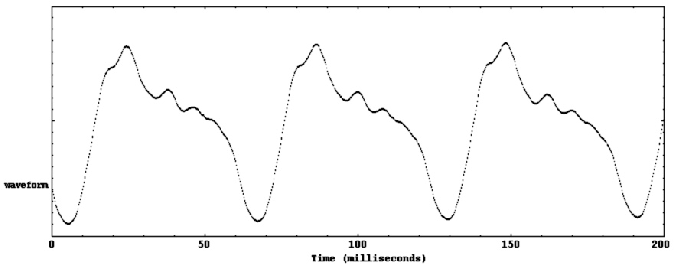
   When a waveform repeats itself, it is known as periodic. The period of the waveform is the shortest possible time after which the waveform always repeats itself.

   Consider the following questions:

   1. Does the waveform appear to repeat?
   2. Is each repeated section of the waveform the same (i.e. is it periodic)?
   3. What does the waveform look like?
   4. Does it look like a pure sine wave or something different?

   Record your observations below:
   

   You should be able to see that the waveform does, indeed, repeat with a constant frequency. This frequency determines the pitch of the sound the string makes. However, the repetition is not exact for real strings because the pluck decays gradually.

2. After you are able to capture a good sample of the waveform in the waveform window, see if you can measure the period and calculate the fundamental frequency. Try to figure out how long it takes for the signal to repeat. The time scale is indicated on the bottom of the waveform window, and each notch corresponds to 10 ms. A reasonable period might be something around 60 ms. For comparison, the period of the waveform in Figure 5 is about 62ms although the waveform repeats itself every 62ms, 124ms, 186ms, 248ms, ...

3. Calculate the fundamental frequency with the following relationship:
   

   $${\textrm{frequency}} = \frac{1}{\textrm{period}},$$ (7)

   
   
   where the period is in seconds and frequency is in Hz (cycles per second). Thus, for example, if the period were 62 ms, the calculation would be as follows:
   

   $$\textrm{frequency} = \frac{1}{0.0062} = 161 \textrm{Hz}$$ (8)

   
   

   Record your your calculated fundamental frequency, in hertz, here:

   Now figure out which note on the piano your computed fundamental frequency is closest to. To compute the fundamental frequency in Hz corresponding to a given piano note number $d$ (where $d = 69$ corresponds to piano note A4 (the A above middle C on the piano)), you can use the following formula:
   

   $$f_0 = 440 \cdot 2^{\left( d - 69 \right)/12},$$ (9)

   
   
   where $f_0$ is the frequency in Hz. Solve this formula for $d$ in order to compute a note number from a given fundamental frequency.

   For reference, a table of fundamental frequencies and corresponding notes can be found at
   http://www.liutaiomottola.com/formulae/freqtab.htm. Record the note which corresponds to your calculated fundamental frequency here: