Coupled Strings in Faust

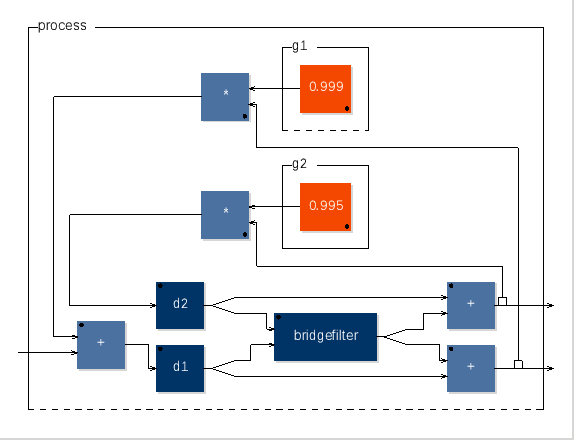
A diagram for two coupled strings is given in [14].¹⁴A Faust template for this block diagram is displayed in Fig.12 and specified as follows:

 import("music.lib");
 g1 = 0.999; g2 = 0.995; P = 200; Pmax = 256; detune = 1;
 d1 = fdelay(Pmax,P-2);
 d2 = delay(Pmax,P*(1.0 - 0.01*detune)-2);
 bridgefilter = + : *(-0.5);
 g = g1;
 stringloop = ( _,+ : ((d2 <: _,_),(d1 <: _,_)) 
     : (_, (bridgefilter <: _,_) ,_) 
     : +,+) ~ (*(g2),*(g1)) ;

 process = stringloop;

where P is the fundamental period, in samples, and $g$ denotes the round-trip filtering on the string during one period. (Placeholder values are given in the Faust listing so it will compile and generate Fig.12.)

Figure 12: Two strings coupled by a general bridge impedance.

Note that the excitation only enters one of the string loops in Fig.12. This corresponds, for example, to plucking the string in the horizontal plane, say (the d1 loop), with the vertical plane (d2 loop) vibrating ``sympathetically''. More generally, the two loops may be excited by varying amounts of the excitation signal, corresponding to a physically inexact excitation plane.

As discussed in [14], the bridgefilter $H_b(z)$ is of the form

$$H_b(z)\mathrel{\stackrel{\Delta}{=}}\frac{2}{2 + R_b(s)/R}$$

where $R$ is the (real, positive) wave impedance of the string, and $R_b(s)$ denotes the bridge driving-point impedance (a positive-real function of the Laplace variable $s$). The special case indicated in the Faust listing above, $H_b(z) = 0.5$, corresponds to $R_b = 2R$, which is similar to the following simplified diagram (shown in Fig.13) when g1 = g2 = g:

  stringloop = (+ <: d2,d1 : + : *(0.5)) ~ *(g);

This simplified coupling algorithm runs about twice as fast as the full algorithm (based on Faust benchmarks using the bench.cpp architecture file).

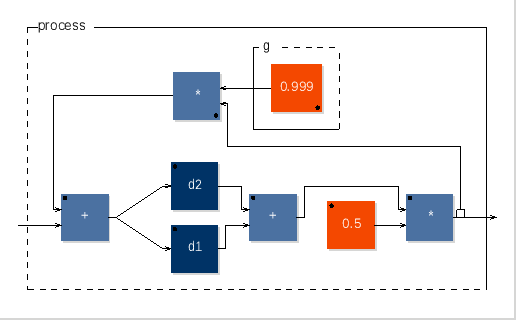Figure 13: Two strings coupled at a real bridge impedance equal to twice the string impedance, i.e., $R_b = 2R$.