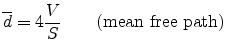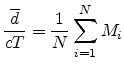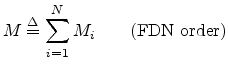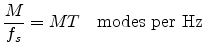Next |
Prev |
Up |
Top
|
REALSIMPLE Top
- Delay line lengths
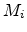 typically mutually prime
typically mutually prime
- For sufficiently high mode density,
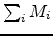 must be sufficiently large.
must be sufficiently large.
- No ``ringing tones'' in the late impulse response
- No ``flutter''
Mean Free Path
where 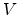 is the total volume of the room, and
is the total volume of the room, and 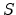 is total surface
area enclosing the room.
is total surface
area enclosing the room.
Regarding each delay line as a mean-free-path delay, the mean free
path length, in samples, is the average delay-line length:
where 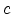 = sound speed and
= sound speed and 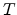 = sampling period.
= sampling period.
This is only a lower bound because many reflections are
diffuse in real rooms, especially at high frequencies
(one plane-wave reflection scatters in many directions)
Mode Density Requirement
FDN order = sum of delay lengths:
- Order = number of poles
- All
 poles are on the unit circle in the lossless prototype
poles are on the unit circle in the lossless prototype
- If uniformly distributed, mode density =
- Schroeder suggests that 0.15 modes per Hz
(when 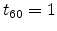 second)
second)
- Generalizing:
- Example: For
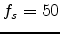 kHz and
kHz and 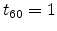 second,
second,
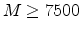
- Note that
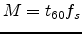 is the length of the FIR filter
giving an exact implementation. Thus, recursive filtering is
about 7 times more efficient by this rule of thumb.
is the length of the FIR filter
giving an exact implementation. Thus, recursive filtering is
about 7 times more efficient by this rule of thumb.
Next |
Prev |
Up |
Top
|
REALSIMPLE Top
Download Reverb.pdf
Download Reverb_2up.pdf
Download Reverb_4up.pdf